Reprezentarea numerelor naturale pe axa numerelor
O dreaptă pe care se fixează un punct, numit origine, un sens de deplasare și un segment numit unitate de măsură se numește axa numerelor.
Fiecărui număr natural îi corespunde pe axă, un punct. Numărul respectiv se numește coordonata punctului. Originea are coordonata zero (0). Axa numerelor ne ajută să comparăm și să ordonăm numerele naturale.
Exemplu:
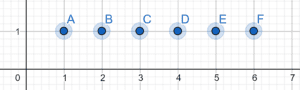
lui 2 îi corespunde B, lui 5 îi corespunde E
Observații:
- Orice număr diferit de 0 se numește nenul; dacă a este un număr natural nenul, se scrie \(a\neq 0\) și se citește „numărul \(a\) este diferit de zero”.
- Urmărind figura se poate observa că oricare două puncte consecutive de pe axa numerelor de află la aceeași distanță unul de altul.
- Pe axă, numerele mai mari sunt așezate în dreapta numerelor mai mici.
Compararea numerelor naturale
Dintre două numere naturale care au un număr diferit de cifre, este mai mare numărul care are mai multe cifre. Dintre două numere naturale care au același număr de cifre, numărul cel mai mare este cel la care întâlnim prima cifră mai mare, când comparăm cifrele de același ordin de la stânga la dreapta.
Exemple:
\(3572\gt 123\)
\(2363572\gt 12363569\)
Semnele folosite în compararea numerelor sunt: \(=, \lt , \gt , \le , \ge\).
Pentru oricare două numere naturale \(a\) și \(b\), dacă \(a\lt b\) sau \(a=b\) se scrie \(a\le b\) și se citește „\(a\) este mai mic sau egal cu \(b\)”; dacă \(a\gt b\) sau \(a=b\) se scrie \(a\ge b\) și se citește „\(a\) este mai mare sau egal cu \(b\)”.
Exemple:
- Numerele naturale mai mici sau egale cu 7 sunt: 0, 1, 2, 3, 4, 5, 6, 7
- Numerele naturale mai mari ca 2001 și mai mici și egale cu 2006 sunt: 2002, 2003, 2004, 2005, 2006.
- Numerele naturale de forma \(\overline{aa}\) mai mici ca 50 sunt: 11, 22, 33, 44.
Ordonarea numerelor naturale
Prin ordonarea numerelor naturale înțelegem scrierea în ordine crescătoare sau descrescătoare a acestor numere. Dintre două numere naturale reprezentate pe axa numerelor, mai mare este cel reprezentat în dreapta celuilalt.
Exemplu:
În șirul numerelor naturale 0, 1, 2, 3 …, 20, 21, 22, …, 54, 55, …, numărul 21 este situat înaintea numărului 54. Se spune ca 21 este mai mic decât 54 și se scrie 21<54 sau că 54 este mai mare decât 21 și se scrie 54>21.
Aproximarea numerelor naturale
Nu întotdeauna este necesar să știm exact toate cifrele unui număr, ci numai ordinul său de mărime. De exemplu, dacă la un concert participă 3160 de spectatori, putem spune că au fost vândute aproximativ 3000 de bilete.
Atunci când folosim, în locul unui număr dat, un alt număr, apropiat de el, spunem că am folosit o aproximare a numărului dat. Există trei tipuri de aproximări: prin lipsă, prin adaos și prin rotunjire.
Aproximarea prin lipsă a unui număr natural la ordinul zecilor (sutelor, miilor, etc.) este cel mai mare număr natural format din zeci (sute, mii, etc.), mai mic sau egal cu numărul respectiv.
Exemple:
- Aproximarea prin lipsă până la zeci a numărului 68734 este 68730
- Aproximarea prin lipsă până la sute a numărului 68734 este 68700
- Aproximarea prin lipsă până la mii a numărului 68734 este 68000
Observație:
Aproximarea prin lipsă a unui număr natural la ordinul zecilor se obține înlocuind ultima cifră a numărului (cifra unităților) cu zero, aproximarea prin lipsă la ordinul sutelor se obține înlocuind ultimele două cifre cu zero, etc.
Aproximarea prin adaos a unui număr natural la ordinul zecilor (sutelor, miilor, etc.) este cel mai mic număr natural format din zeci (sute, mii, etc.), strict mai mic decât numărul respectiv.
Exemple:
- Aproximarea prin adaos până la zeci a numărului 68734 este 68740
- Aproximarea prin adaos până la sute a numărului 68734 este 68800
- Aproximarea prin adaos până la mii a numărului 68734 este 69000
Rotunjirea numerelor naturale
Rotunjirea unui număr natural la ordinul zecilor (sutelor, miilor, etc.) este aproximarea la ordinul considerat, prin lipsă sau prin adaos, cea mai apropiată de numărul respectiv. În cazul în care cele două aproximări sunt la fel de apropiate de număr, pentru rotunjire se ia în considere aproximarea prin adaos.
Exemple:
- Rotunjirea până la zeci a numărului 68734 este 68730
- Rotunjirea până la sute a numărului 68734 este 68700
- Rotunjirea până la mii a numărului 68734 este 69000