Relații între mulțimi
Două mulțimi sunt egale dacă au aceleași elemente. Dacă \(A\) și \(B\) sunt două mulțimi egale, notăm \(A=B\), iar dacă nu sunt egale notăm \(A\neq B\).
Fie \(A\) și \(B\) două mulțimi. \(A\) este inclusă în \(B\) dacă orice element al mulțimii \(A\) este și element al mulțimii \(B\). Se scrie \(A\subset B\). Se mai spune că \(B\) include pe \(A\). În acest caz se spune despre \(A\) că este o submulțime a lui \(B\).
Se consideră că mulțimea \(\emptyset\) este o submulțime a oricărei mulțimi \(A\).
O mulțime este inclusă în ea insăși. Deci \(A\subset A\), oricare ar fi mulțimea \(A\).
Orice mulțime \(A\) are submulțimile \(A\) și \(\emptyset\), numite submulțimi improprii. Orice submulțime a lui \(A\), diferită de \(A\) și \(\emptyset\), dacă există, se numește submulțime proprie a lui \(A\).
Mulțimea tuturor submulțimilor unei mulțimi \(A\) formează mulțimea părților mulțimii \(A\) și se notează cu \(P(A)\).
Două mulțimi sunt egale dacă fiecare dintre ele este o submulțime a celeilalte mulțimi: \(A=B\) dacă și numai dacă \(A\subseteq B\) sau \(B\subseteq A\).
Observații:
Mulțimea care are ca elemente toate numerele naturale este numită mulțimea numerelor naturale și se notează cu \(\mathbb{N}\).
Așadar \(\mathbb{N}=\left\{ 1,2,3,… \right\}\)
Mulțimea ale cărei elemente sunt toate numerele naturale mai puțin cifra 0 se numește mulțimea numerelor naturale nenule.
\(\mathbb{N}^{*}=\left\{ 1,2,3,… \right\}\)
Deci \(\mathbb{N}^{*}\subset \mathbb{N}\)
Dacă notăm cu n numărul submulțimilor finite \(A\), atunci \(n=2^{card A}\)
Exemplu:
Mulțimea \(A=\left\{ 1,2,3 \right\}\) are \(2^{3}=8\) submulțimi: \(\emptyset , \left\{ 1 \right\},\left\{ 2 \right\},\left\{ 3 \right\},\left\{ 1,2 \right\},\left\{ 2,3 \right\},\left\{ 1,3 \right\},\left\{ 1,2,3 \right\}\)
Exerciții rezolvate
Operații cu mulțimi
Reuniunea
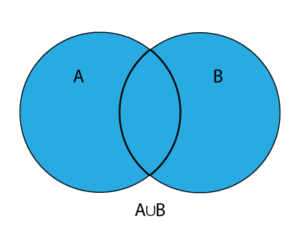
Reuniunea a două mulțimi \(A\) și \(B\) este mulțimea elementelor care aparțin cel puțin uneia dintre ele: \(A\cup B=\left\{ x | x\in A \text{ sau } x\in B \right\}\)
Exemplu:
Fie două mulțimi \(A=\left\{ 1, 2, 3 \right\}\) și \(B=\left\{ 3, 4, 5 \right\}\), reuniunea lor este \(A\cup B=\left\{1,2,3,4,5 \right\}\)
Intersecția
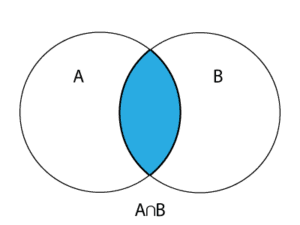
Intersecția a două mulțimi \(A\) și \(B\) este mulțimea elementelor comune celor două mulțimi: \(A\cap B=\left\{ x | x\in A \text{ si } x\in B \right\}\).
Dacă \(A\cap B=\emptyset\) , atunci mulțimile \(A\) și \(B\) sunt mulțimi disjuncte.
Exemplu:
Fie două mulțimi \(A=\left\{ 1, 2, 3 \right\}\) și \(B=\left\{ 3, 4, 5 \right\}\), intersecția lor este \(A\cap B=\left\{3 \right\}\)
Mulțimi disjuncte
Fie două mulțimi \(A=\left\{ 1, 2, 3 \right\}\) și \(B=\left\{ 4,5,6\right\}\), intersecția lor este \(A\cap B=\emptyset\)
Diferența
Fie \(A\) și \(B\) două mulțimi. Mulțimea formată din elementele lui \(A\) care nu sunt elemente ale lui \(B\) se numește diferența dintre mulțimea \(A\) și \(B\): \(A-B=\left\{x|x\in A\ \text{si } x\notin B\right\}\). Și invers, mulțimea formată din elementele lui \(B\) care nu sunt elemente ale lui \(A\) se numește diferența dintre mulțimea \(B\) și \(A\): \(B-A=\left\{x|x\notin A\ \text{si } x\in B\right\}\)
Exemplu:
Fie două mulțimi \(A=\left\{ 1, 2, 3 \right\}\) și \(B=\left\{ 3, 4, 5 \right\}\), diferența dintre mulțimea \(A\) și \(B\) este \(A- B=\left\{1,2 \right\}\). Diferența dintre mulțimea \(B\) și \(A\) este \(B-A=\left\{4,5 \right\}\).
Proprietățile operațiilor de reuniuni și intersecții
Asociativitatea:
\(\left( A\cup B \right)\cup C=A\cup \left( B\cup C \right)\)
sau
\(\left( A\cap B \right)\cap C=A\cap \left( B\cap C \right)\)
Comutativitatea:
\(A\cup B=B\cup A\)
sau
\(A\cap B=B\cap A\)
Distributivitatea:
- reuniunii față de intersecție:
\(A\cup \left( B\cap C \right)=\left( A\cup B \right)\cap \left( A\cup C \right)\)
- intersecției față de reununiune:
\(A\cap \left( B\cup C \right)=\left( A\cap B \right)\cup \left( A\cap C \right)\)
Principiul includerii și excluderii
- pentru oricare două mulțimi \(A\) și \(B\) avem:
\( card A\cup B=card A+card B-card A\cap B\)
Observații:
- Diferența și produsul cartezian nu sunt, în general, operații comutative:
\(A-B\neq B-A; A\times B\neq B\times A\)
- Scrierea ca reuniune de mulțimi disjuncte:
\(A\cup B=\left( A-B \right)\cup \left( A\cap B \right)\cup \left( B-A \right)\)