Mulțimi - descriere, notații, reprezentări
Mulțimea este o colecție de obiecte bine determinate și distincte numite elementele mulțimii.
Mulțimile se notează cu litere mari \((A, B, C, M, N…)\), iar elementele mulțimii se notează cu litere mici, simboluri, numere. Elementele unei mulțimi se scriu între acolade, despărțite de virgulă, într-o ordine oarecare. Într-o mulțime un element este scris o singură dată.
Între un element și o mulțime vorbim de relația de apartenență, dacă elementul se regăsește în mulțime și folosim simbolul \(\in\), sau de relația de neapartenență, dacă elementul nu se regăsește în mulțime și folosim simbolul \(\notin\).
Dacă \(A\) este o mulțime și \(x\), un element al său, atunci vom scrie \(x\in A\) și vom citi „\(x\) aparține lui \(A\)”. Dacă \(x\) nu este un element al mulțimii \(A\), atunci vom scrie \(x\notin A\) și vom citi „\(x\) nu aparține lui \(A\)”.
Exemplu:
Dacă \(A= \left\{ 0,2,4,6,8 \right\}\), avem \(0\in A\), \(2\in A\), \(4\in A\), \(6\in A\), \(8\in A\) dar \(5\notin A\), \(9\notin A\)
O mulțime poate fi dată în trei moduri:
Exemplu:
\(A= \left\{ 0,2,4,6,8 \right\}\)
Citim: „Mulțimea \(A\) este formată din elementele 0, 2, 4, 6 și 8”.
2. Cu ajutorul diagramei Venn-Euler; în acest caz, mulțimea poate fi ilustrată desenând o curbă închisă și scriind în interiorul ei elementele corespunzătoare.
Exemplu:
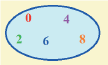
2. Enunțând o proprietate caracteristică elementelor mulțimii (pe care o are oricare element al mulțimii și nu o are nici un alt element car nu aparține mulțimii).
Exemplu:
\(A= \left\{ x | x \text{ este cifra para} \right\}\)
Citim: „Mulțimea \(A\) este formată din elemente cu proprietatea că \(x\) este o cifră pară”.
Mulțimi finite. Mulțimi infinite
Mulțimile care au un număr finit (limitat) de elemente se numesc mulțimi finite, iar mulțimile care au un număr infinit (nelimitat) de elemente se numesc mulțimi infinite.
Exemple:
- Mulțimea numerelor naturale este infinită
- Mulțimea elevilor dintr-o școală este finită
- Mulțimea numerelor pare este infinită
- Mulțimea numerelor cu două cifre este finită
Mulțimea care nu are nici un element se numește mulțime vidă și se notează cu simbolul \(\emptyset\).
O mulțime numerică este o mulțime ale cărei elemente sunt numere.
O mulțime nenumerică este o mulțime care nu este numerică.
Numărul de elemente ale mulțimi \(A\) se numește cardinalul mulțimii \(A\) și se notează \(card A\).
Exemplu:
Mulțimea \(A= \left\{ 0,2,4,6,8 \right\}\) are 5 elemente și scriem \(card A = 5\)
\(card \mathbb{N}^{*} = \infty\)